Directions: Click on the images to begin the animation.
A) RANDOM WALK ANIMATION
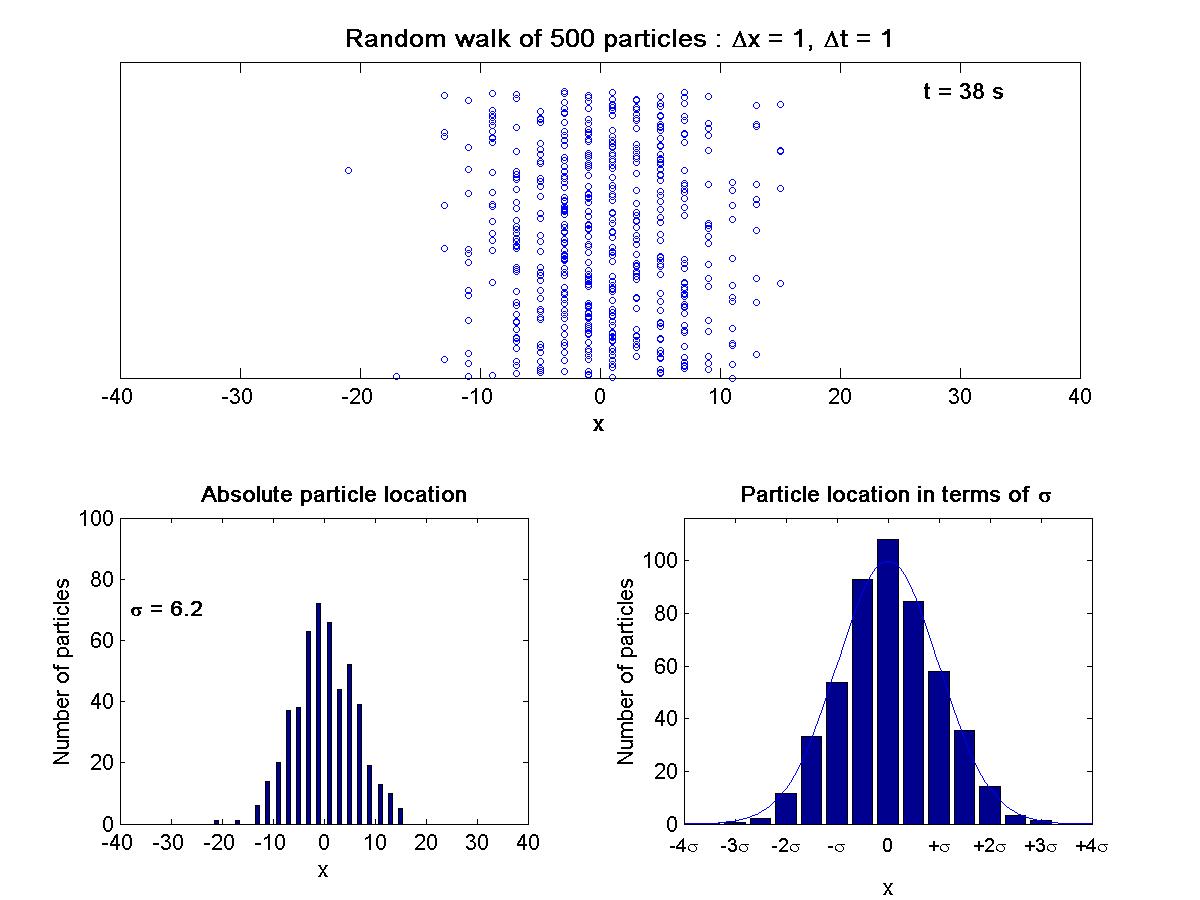
Diffusion Animation
This animation shows the motion of 500 particles in a one-dimensional random walk with step size X = 1 in time t = 1. This random walk animation mimics the effect of Fickian Diffusion. For some background and thought problems pertaining to this animation, review the theory (page 4) behind this conceptual model of diffusion.
* Note to Unix users: the animation opens up behind active windows
B) ILLUSTRATION OF TOTAL DERIVATIVE: STEADY TEMPERATURE FIELD
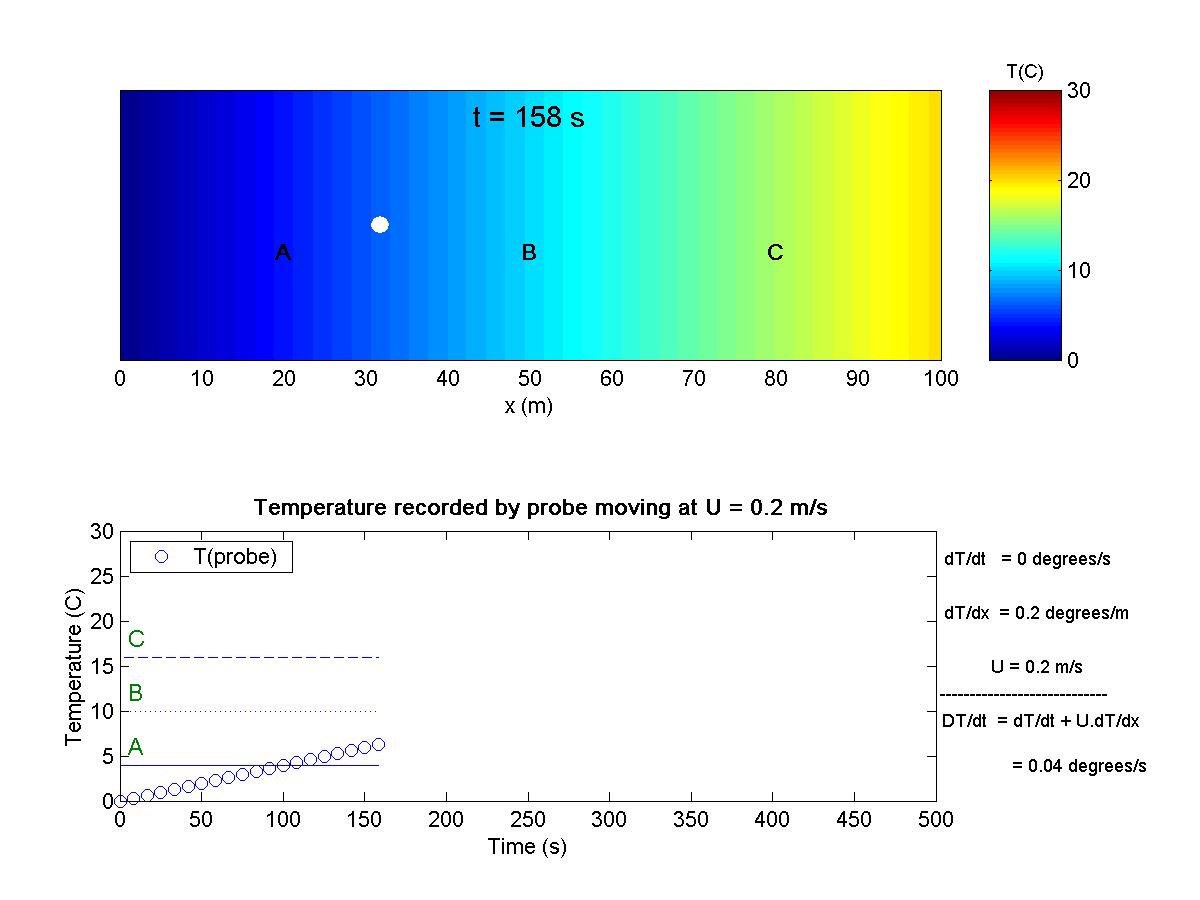
This animation shows a one-dimensional system with a spatial gradient of temperature, T(x). A temperature probe (white dot) moves with the flow, making a Lagrangian observation. The probe records the material (total) derivative. Go to the theory section (page 6) for some background material on the concept of the total derivative.
* Note to Unix users: the animation opens up behind active windows
C) ILLUSTRATION OF TOTAL DERIVATIVE: UNSTEADY TEMPERATURE FIELD
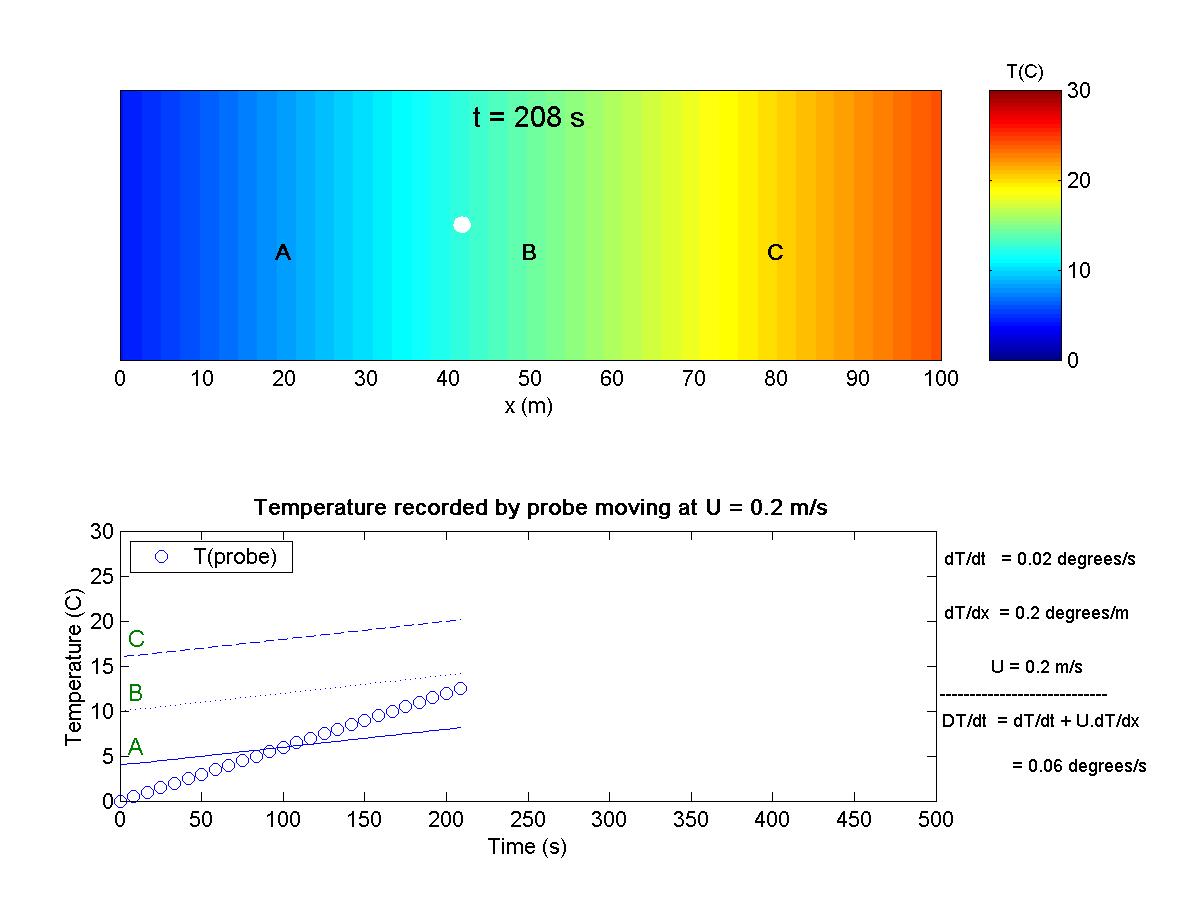
This animation shows a one-dimensional system with an unsteady temperature field, T(x,t). A temperature probe is moving through the flow at velocity u, and it records the material derivative. Three additional probes are located at the fixed positions A, B, and C. Go to the theory section (page 6) for some background material on the concept of the total derivative.
* Note to Unix users: the animation opens up behind active windows
D) STEADY, SPATIALLY ACCELERATING FLOW IN A PIPE
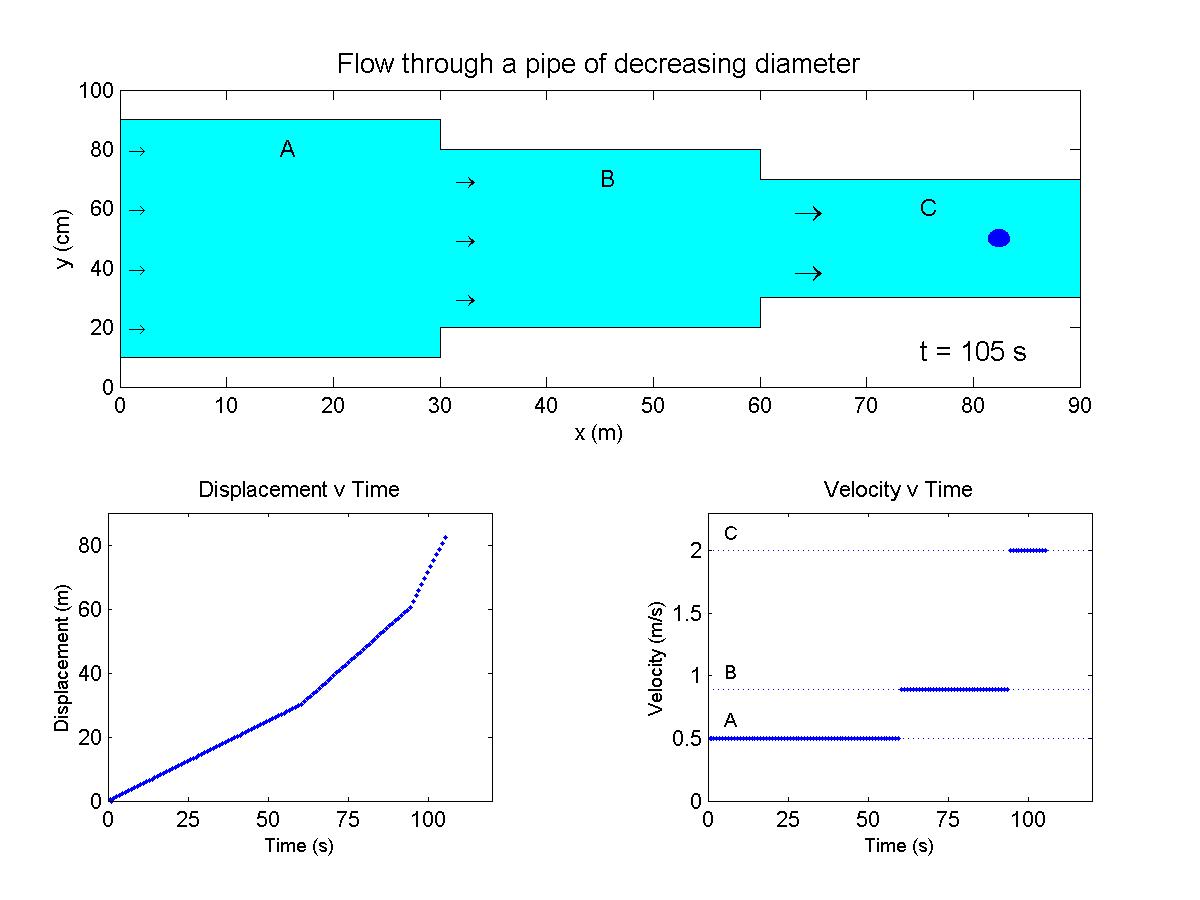
In this animation, flow through a pipe accelerates downstream as the pipe cross-section decreases. The velocity and displacement of a probe moving with the flow are shown versus time. For some background and thought problems pertaining to this animation, review the theory (page 6) behind spatially accelerating flows.
* Note to Unix users: the animation opens up behind active windows
MATLAB® is a trademark of The MathWorks, Inc.