-

-
Courses
Find courses by:
Collections
- About
- Donate
- Featured Sites
This is an archived course. A more recent version may be available at ocw.mit.edu.
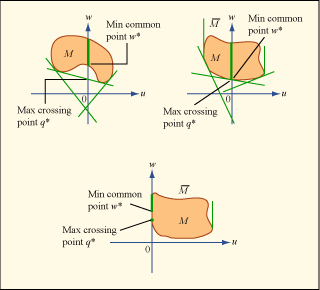
Min common/max crossing problems. See Lecture 9 for more information. (Image by MIT OpenCourseWare.)
Prof. Dimitri Bertsekas
6.253
Spring 2010
Graduate
This course will focus on fundamental subjects in (deterministic) optimization, connected through the themes of convexity, geometric multipliers, and duality. The aim is to develop the core analytical and computational issues of continuous optimization, duality, and saddle point theory using a handful of unifying principles that can be easily visualized and readily understood.
The mathematical theory of convex sets and functions will be central, and will allow an intuitive, highly visual, geometrical approach to the subject. This theory will be developed in detail and in parallel with the optimization topics.
The first part of the course develops the analytical issues of convexity and duality. The second part is devoted to convex optimization algorithms, and their applications to a variety of large-scale optimization problems from resource allocation, machine learning, engineering design, and other areas.