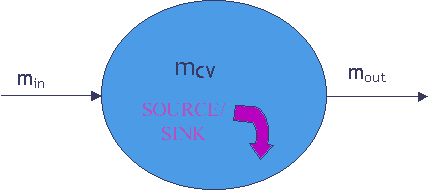
This section discusses the law of conservation of mass within a control volume, expressed in both integral and differential forms. Mathemical descriptions of advective and diffusive fluxes into/out of a control volume are shown, the end result being the all-important mass transport equation. The concept of the total derivative is also introduced, allowing us to relate Eulerian (fixed position) and Lagrangian (moving with the flow) perspectives. Two animations further explain the total derivative, showing the temporal temperature change of a probe moving through a spatial temperature gradient. The example problems require application of both forms of the law of conservation of mass to solve transport problems in both industrial and environmental contexts.